Fast and Accurate Personalized Recommendation with Indexing
In a previous blog post, we introduce the problem of top-K recommendation retrieval using Matrix Factorization (MF). We also highlight the importance of indexing structures as a faster alternative to an exhaustive search in this context.
Issues with Indexing for Top-K Maximum Inner Product Search (MIPS)
Traditional indexing structures are designed for similarity search with metric functions such as the Euclidean distance or the angular distance. Inner product kernel of matrix factorization methods, however, is not a proper metric. Given a point x, one can always find another point y that is more similar to x than x to itself according to the inner product score. This violates the triangle inequality property of a metric, which may lead to inaccurate retrieval of the true top-K recommendations after indexing.
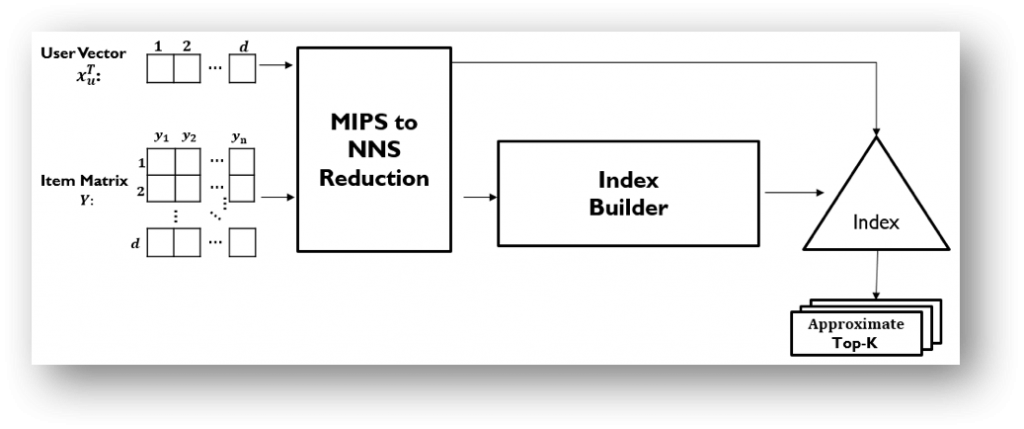
1. Reducing MIPS to a Nearest Neighbor Search
One solution is to reduce MIPS to an equivalent nearest neighbour search task (MIPS-to-NNS), which can be solved efficiently by existing indexing structures. This idea has been introduced as a two-step process for MF-based top-K recommendation retrieval. The user and item vectors are transformed and augmented so that solving MIPS in the original space is equivalent to solving nearest neighbour search in the transformed space. However, the transformed vectors may be concentrated in one region causing an imbalanced distribution of data in the new space, which may in turn affect downstream approximate nearest neighbour search tasks (see “Indexable Probabilistic Matrix Factorization for Maximum Inner Product Search” at AAAI 2016 for more detailed explanation).
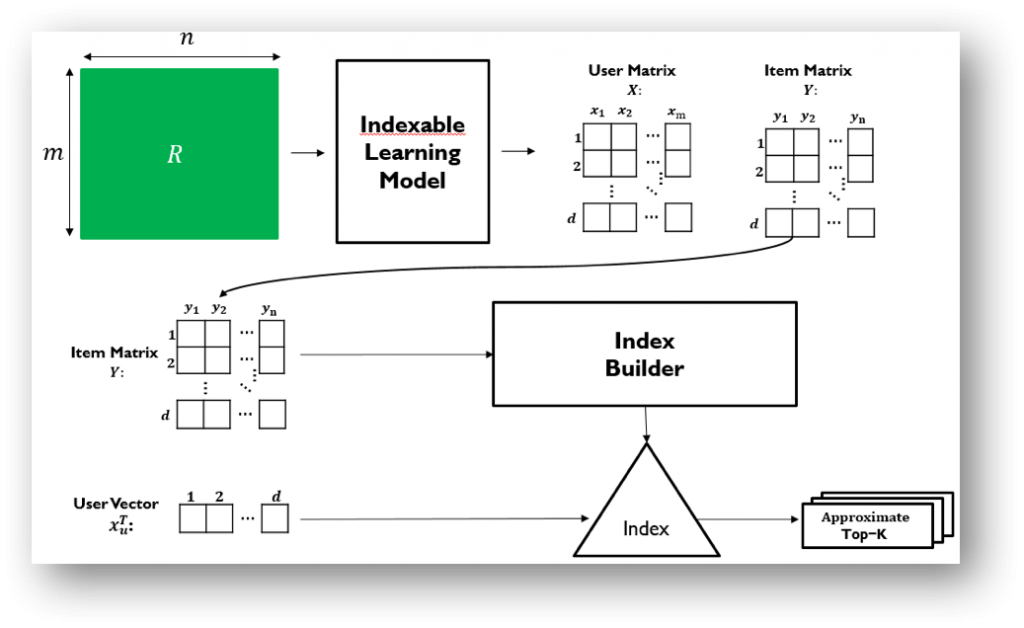
2. Indexable Representation Learning
Another solution is indexable representation, which learns user and item vectors that are compatible with the indexing structures. Indexable representation learning models replace the inner product kernel with a proper distance metric function such as the Euclidean distance (see “Collaborative Filtering via Euclidean Embedding” at RecSys 2016) or the angular distance (see “Indexable Bayesian Personalized Ranking for Efficient Top-K Recommendation” at CIKM 2017). In these metric spaces, top-K recommendation retrieval can be solved efficiently with structures such as Locality Sensitive Hashing (LSH), spatial trees, or inverted index. Also, as it does not require augmenting user and item vectors, indexable representation models can avoid the imbalanced data distribution issue of the MIPS-to-NNS approach.
Moving forward, it is a promising approach to design unified learning frameworks that factor the structural properties of the retrieval-efficient component in learning user and item vectors (i.e., preference elicitation component). This would allow the recommendation pipeline to better preserve the accuracy of the preference elicitation models, and at the same time to exhibit the efficiency of retrieval-efficient structures. For instance, in our recent work “Stochastically Robust Personalized Ranking for LSH Recommendation Retrieval” at AAAI 2020, we trace the incompatibility issue to the stochastic nature of randomized hash function of LSH. We then introduce Stochastically Robust Personalized Ranking (or SRPR for short) model that learns from implicit feedback to derive the user and item vectors that are robust to the stochasticity of randomly generated LSH hash functions. SRPR thus achieves both efficient retrieval and accurate top-K recommendation when LSH is the designated indexing structure.
If you want to gain more hands-on experience for efficient recommendation with indexing, please check out this tutorial.
Have fun learning with Preferred.AI!




