A Quest for Fast Personalized Recommendation
Personalized recommender systems attempt to generate a limited number of item options (e.g., products on Amazon, movies on Netflix, or videos on Youtube, etc.) that are curated for each individual customer. The necessity of such systems is driven by the explosion of online choices, which makes it difficult for each customer to investigate every option. Therefore, more and more product and service providers are now relying on these systems to improve customer experience and conversion on their websites.
An established and prevalent technique for personalized recommendation is collaborative filtering based on matrix factorization (MF), which attempts to learn customers’ preferences from their historical activities. Let’s assume that there are m users, denoted as U and n items, denoted as I. Typically, a classic matrix factorization model consists of two phases:
- Learning: this phase analyses customers’ historical activities, represented by a sparse matrix R of size m x n, to learn their preferences. Each customer u is represented by a d-dimensional vector xu and each item i is represented by a d-dimensional vector yi, where d is the hypothetical number of factors that explain the behaviour of each customer. The degree of preference of a customer u for an item i is modelled as the inner product score (xu)Tyi. A higher inner product score implies a higher chance of the customer u to prefer the item i.
- Retrieval: given the output vectors from the learning phase, to arrive at a personalized recommendation list for customer u, we need to identify the top-K items in I that have the highest inner product scores to xu. Figure 1 illustrates the pipeline of top-K MF recommendation retrieval, in which Y denotes the item matrix where each row represents an item vector.
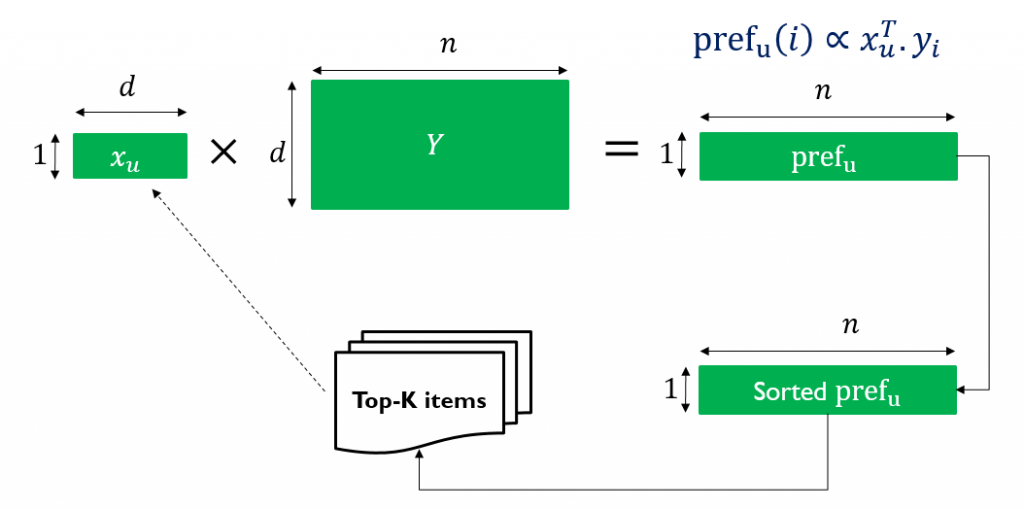
Figure 1: Top-K Retrieval of Matrix Factorization Models
The challenge of the learning phase is how to design effective algorithms that can learn from the data at the scale of millions of customers and items. This problem has been studied extensively in the research literature. On the other hand, the challenge of the retrieval phase is speed, due to the real-time nature of the task: upon the arrival of a targeted customer u, the system needs to quickly generate top-K items with highest inner product scores to xu be recommended for u.
Formally, the above problem of finding the top-K MF recommendations can be stated as follows:
(Maximum Inner Product Search-MIPS) Given a customer vector xu, determine the item i such that:
i=\mathrm{argmax}_{j \in I} x_u^T y_jA straightforward solution for MIPS is to compute the inner product between xu and all item vectors {y1, y2, …, ym} and rank these scores. However, such solution scales linearly with the number of items, which incurs the prohibitive cost given current number of items in today large-scale systems (see References [1], [2], [3] for more detailed analysis). To achieve real-time personalized recommendation, we shall look for faster alternatives to solve the MIPS problem efficiently, specifically those who can avoid examining all items in I. In this post, we will explore such a solution, namely indexing.
Indexing for Matrix Factorization Recommendation Retrieval
As top-K MF recommendation retrieval can be considered as top-K similarity search task with inner product as the similarity function, one can apply various approximate similarity search techniques such as indexing, quantization, or graph similarity to improve the speed of the search process. In this post, we primarily focus on indexing as it offers several appealing advantages: one-time pre-processing of item vectors, parallelizable search, and scale linearly with the number of items, etc.
Figure 2 depicts two steps of a top-K recommender system with the aid of indexing structures:
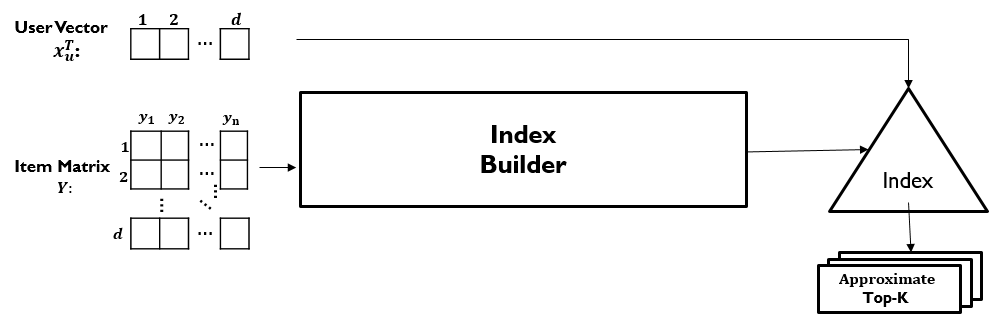
Figure 2: Indexing Approach for Efficient Top-K Retrieval
- Index construction: process and store the item vectors Y in a data structure (e.g., hash tables, binary search trees, etc.) so that similar item vectors are stored closely in the data structure (e.g., on the same buckets of the hash tables or the same leaf nodes of the binary search tree. etc.).
- Retrieval: Given the built data structure, a search for the top-K most similar items to a customer vector xu, i.e., top-K recommendations can be performed in order of magnitude faster than naïve exhaustive search. This is primarily due to the property of indexing structures, which can automatically remove potential irrelevant items with high confidence and reduce the number of item candidates for inner product computation and ranking.
The benefit of indexing comes at the cost of constructing the data structures to store the item vectors in new formats that support efficient similarity search, which is a one-time cost to be amortized over the many query instances.
Though having several advantages, a factor for consideration when using indexing structures for top-K recommendation is the growth rate of the systems. As customer preferences may change over time, new items appear, or old items are removed, maintaining a retrieval-efficient structure would require constant updates (e.g., insertion, deletion, or even re-build).
In the next part, we will investigate further some issues with using indexing for top-K MIPS as well as discuss some promising solutions.
References
[1] Koenigstein, Noam, Parikshit Ram, and Yuval Shavitt. “Efficient retrieval of recommendations in a matrix factorization framework.” Proceedings of the 21st ACM international conference on Information and knowledge management. 2012.
[2] Le, D. D., & Lauw, H. W. (2017, November). Indexable Bayesian Personalized Ranking for Efficient Top-k Recommendation. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management (pp. 1389-1398). ACM.
[3] Le, D. D., & Lauw, H. W (2020, Feb). Stochastically Robust Personalized Ranking for LSH Recommendation Retrieval, In Proceeding of the 34thAAAI Conference on Artificial Intelligence (AAAI’20), Feb 2020.




